TO CALCULATION OF OPTIMIZATION PROBLEM OF THE CHEMICAL PROCESS IN ISOTHERMIC REACTOR IDEAL REMOVAL

O.O. Onyshchuk; Zh. Kormosh

O.O. Onyshchuk Lesya Ukrainka Eastern European National University
Zh. Kormosh Lesya Ukrainka Eastern European National University

Keywords: ideal mixing model, concentration, half-division method (dichotomy method)

Abstract

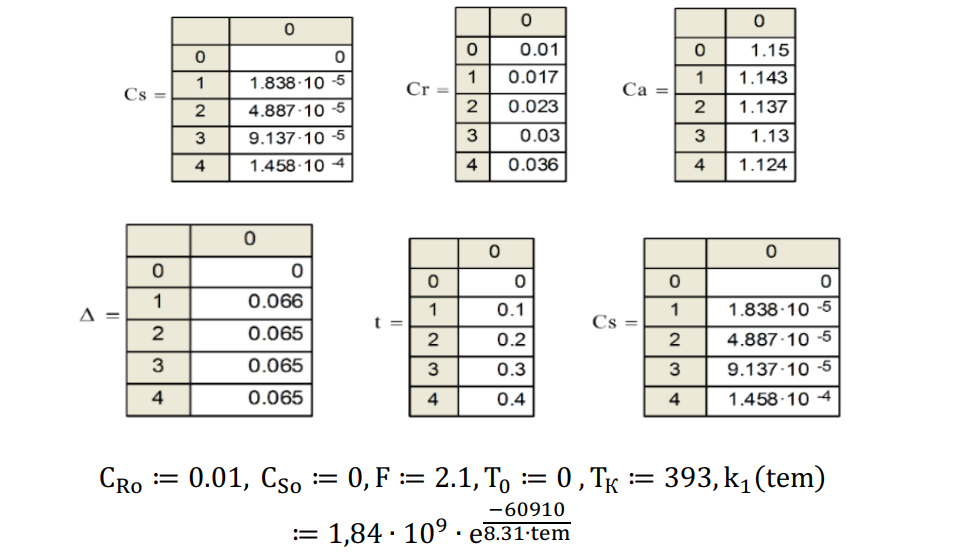
In article, it was dealed with the model of ideal mixing and idealized flow entering the reactor which instantly distributed throughout the volume as a result of the complete (ideal) mixing of the medium particles. It was used the half-division method (dichotomy method) of the intervals in the MathCAd medium. It was used the system of algebraic equations of material and thermal equilibrium. We have determined the optimal concentration of the components of the reaction in the stationary mode. Optimization of the problem of the output of the target product for the isothermal thermal regime and the chemical process gave the possibility to obtain the maximum value of the function at given points and to calculate the residence time of the substances in the reaction at each reaction interval depending on the change of the concentration of the reactant substance for the chosen chemical process and the given coefficients.

References

Bondar, A.G. (1973). Mathematical modeling in chemical technology. Кyiv: Vyshcha shkola.

Boyarinov, A.I. & Kafarov, V.V. (1985). Methods of optimization in chemical technology. Moscow: Chemistry.

Boyarinov, A.I. (1975). Optimization methods in chemical technology. Moscow: Chemistry.

Venikov, V.A. (1966). The theory of similarity and modeling in relation to the tasks of the electric power industry. Moscow: Higher School.

Gartman, T.N. & Klushin, D.V. (2006). Fundamentals of computer modeling of chemical and technological processes: Textbook manual for universities. Moscow: ICC "Akademkniga".

Gunich, S.Т. & Yanchukovskaya, E.О. (2010). Mathematical modeling and computer calculation of chemical-technological processes. Examples and tasks. Part I: Studies allowance. Irkutsk: Publishing House of IrSTU.

Franks, R. М. (1971). Mathematical modeling in chemical technology. Moscow: Chemistry.

Zakheim, A. Yu. (1982). Introduction to the simulation of chemical-technological processes. Moscow: Chemistry.

Kafarov, V. V. Perov, V.V, & Kafarov, V.P. (1974). Principles of mathematical modeling of chemical-technological systems. Moscow: Chemistry.

Kafarov, V.V. (1971). Methods of Cybernetics in Chemistry and Chemical Technology. Moscow: Chemistry.

Lobour, M.V. (2004). Computer systems of the project. Theory and practice. Lviv: Lviv Politechnika.

Maslov, V.P., Danilov, V.G., & Volosov, K.A. (1987). Mathematical modeling of heat and mass transfer processes. Evolution of dissipative structures. Moscow: Science. Ch. Ed.

Samolov, N.A. (2005). Modeling in chemical and calculation of reactors: Ucheb.posobie: Ufa OOO "Monograph".

Slinko, M.G. (1968). Modeling of chemical reactors. Novosibirsk: Science, Siberian Branch.

Tovazhnyanskiy, L.L. (2005). Computational mathematics and programming in chemical technology. Kharkov: NTU "KhPI".