МОДЕЛЮВАННЯ ПОГРАНИЧНОГО ШАРУ ЗА ЛАМІНАРНОГО Й ТУРБУЛЕНТНОГО РЕЖИМІВ РУХУ НЬЮТОНІВСЬКОЇ РІДИНИ У ГНУЧКОМУ ТРУБОПРОВОДІ
Анотація
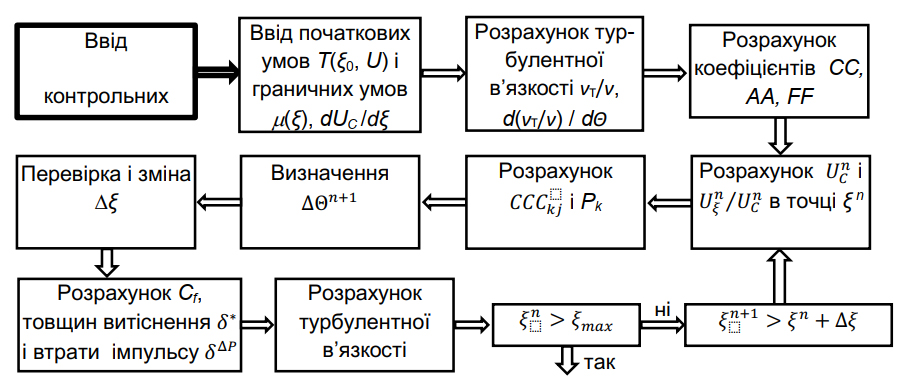
Розглянуто моделювання параметрів пограничного шару для Ньютонівських рідин за ламінарного і турбулентного режимів руху. Виходячи із рівнянь Прандтля, методу Гальоркіна, сформованого тридіагональну систему рівнянь, що зв’язує значення функцій у точці сітки n+1 поперек пограничного шару. Числовим методом за алгоритмом Томаса розраховані значення Ujn+. Значення швидкостей Vjn+1 визначено з рівняння нерозривності інтегруванням поперек пограничного шару. Моделювання турбулентного пограничного шару проведено на основі рівняння Навьє-Стокса в безрозмірній формі числовим метод Дородницина. Наведено результати моделювання розподілу швидкостей і товщини пограничного шару на ділянці трубопроводу 0.8-1.5 м від початку трубопроводу за витрат до 0.1 кг/с.
Посилання
He, S. & Ariyaratne, C. (2011). Wall shear stress in the early stage of unsteady turbulent pipe flow. Journal of Hydraulic Engineering, 137(5), 606–610.
Sundstrom, L.R.J. & Cervantes, M.J. (2018). On the Similarity of Pulsating and Accelerating Turbulent Pipe Flows. Flow, Turbulence and Combustion, 100 (2), 417- 436. https://doi.org/10.1007/s10494-017-9855-5
Kong, R. & Kim, S. (2015, August - September). Characterization of Horizontal Airwater Two-Phase Flow. The 16th International Topical Meeting on Nuclear Reactor Thermal Hydraulics (NURETH-16). (pp. 5559-5572). Chicago / USA.
Offor, U. H. & Alabi, S. B. (2016). An Accurate and Computationally Efficient Explicit Friction Factor Model. Advances in Chemical Engineering and Science, 6, 237-245. http://dx.doi.org/10.4236/aces.2016.63024 (in
Medina, Y. C., Fonticiella, O. M. C. & Morales O. F. G. (2017). Design and modelation of piping systems by means of use friction factor in the transition turbulent zone. Mathematical Modelling of Engineering Problems, 4 (4), 162-167. DOI: 10.18280/mmep.040404
Azizi, N., Homayoon, R., & Hojjati, M. R. (2018). Predicting the Colebrook-White friction factor in the pipe flow by new explicit correlations. Journal of Fluids Engineering, 141 (5), doi:10.1115/1.4041232
Pimenta, B. D., Robaina, A. D., Peiter, M. X., Mezzomo, W., Kirchner, J. H. & Ben, L. H. B. (2018). Performance of explicit approximations of the coefficient of head loss for pressurized conduits. Brazilian Journal of Agricultural and Environmental Engineering (Revista Brasileira de Engenharia Agrícola et Ambiental), 22 (5), 301-307. Retrieved from http://www.agriambi.com.br
Tarek, A. Ganat, & Meftah Hrairi. (2018). Gas–Liquid Two-Phase Upward Flow through a Vertical Pipe. Influence of Pressure Drop on the Measurement of Fluid Flow Rate, Energies (MDPI), 11 (11), 1-23. doi:10.3390/en11112937
Brkic, D. & Praks, P. (2018). Unified Friction Formulation from Laminar to Fully Rough Turbulent Flow. Applied Sciences, 8(11), 20-36. doi: 10.3390/app8112036
Ortiz-Vidal, L. E., Mureithi, N. & Rodriguez, O. M. H. (2013, May). Friction Factor in TwoPhase Gas-Liquid Pipe Flow. 8-th International Conference on Multiphase Flow ( ICMF-2013) Jeju / Korea. Retrieved from
https://www.researchgate.net/publication/237079232
Lukman, S. & Oke, I. A. (2017). Accurate Solutions of Colebrook-White’s Friction Factor Formulae. Nigerian Journal of Technology (NIJOTECH), 36(4), 1039–1048. Nigeria.
Landau, L.D., & Lifshitz, E.M. (1988). Theoretical physics. Hydrodynamics. Moscow: Nauka.
Fletcher, C. A. J. (1988). Computational Techniques for Fluid Dynamics 1: Fundamental and General Techniques. Springer-Verlag, Heidelberg, Berlin.
Lojciansky, L.G. (1950). Fluid and gas mechanics. Moscow: Gosizdat of technical and theoretical literature.
Dorodnitsyn, A.A. (1960). On one method for solving the laminar boundary layerequations. Applied mechanics and technical physics, 3. 111-118.
